a33
Specialised Contributor
- Joined
- Sep 24, 2009
- Messages
- 1,252
- Reaction score
- 720
- Points
- 113
- Age
- 63
- My Satellite Setup
-
XSAT410
Rebox RE-9000
- My Location
- The Netherlands
I have some questions about multifeed installation and multifeedbrackets, wanting to understand the principles behind it/them better.
Q1.
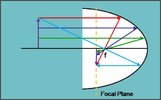
What is the best form of a multifeed bracket in the horizontal plane: straight, curved, … ?
Of course in the vertical plane a multifeed bracket should mirror the Clarke Belt, and thus be curved. But what about the horizontal plane?
I read somewhere about parabolas as optical mirrors, that the focal line is a straight line.
However, there are many multifeed brackets that are curved towards the dish.
So this confuses me: What is the better fit?
And if the focal line is curved, what is the radius of the curve? Is it the same as the focal distance, or twice the focal distance?
For small separations of LNBs this is a minor problem, but for bigger distances the effect might be noticeable. And I would like to understand the theory behind it.
Q2.
What should theoretically be the aiming point of the LNBs?
On a straight multifeed bracket you often see them pointing straight towards the dish, on a curved multifeed bracket you often see them pointing towards the middle of the dish.
Thinking about the G-spot of an offset dish: shouldn't the LNBs also in this case split the opening angle in half, and shouldn't the LNBs point to their own horizontal G-spot?
Q3.
What is the most exact way to calculate the distance between LNBs?
I've seen 3 different ways to calculate the distance between LNBs for multifeed installations.
All are dependent on the focal distance (or distance to the G-spot for offset dishes) and on the difference in Azimuth of the two satellites:
a. distance = fG x sin(dA)
b. distance = fG x ( (dA x PI) / 180) (that is: in radials)
c. distance = fG x tan (dA)
[focal distance = fG, Azimuth difference = dA]
In this order they go from smallest to biggest number.
Till about 15 degrees difference in azimuth they have similar outcomes, but with bigger angles the differences become bigger. Which is the best formula for bigger azimuth differences?
Q4.
Extra question: Would the answers to the questions above be different for multifocus dishes, such as Visiosat (Big) BiSat or Maximum E-85?
For purely toroid dishes, I know that the focal line is curved away from the dish, and that the LNBs look away from the middle of the dish. So is a multifocus dish somewhere between a 'normal' dish and a toroid dish? What kind of focal line, where to aim your LNBs?
This has become a rather long post, but I hope to get some good answers, and to understand the principles of multifeed reception better!
Greetz,
A33
Q1.
What is the best form of a multifeed bracket in the horizontal plane: straight, curved, … ?
Of course in the vertical plane a multifeed bracket should mirror the Clarke Belt, and thus be curved. But what about the horizontal plane?
I read somewhere about parabolas as optical mirrors, that the focal line is a straight line.
However, there are many multifeed brackets that are curved towards the dish.
So this confuses me: What is the better fit?
And if the focal line is curved, what is the radius of the curve? Is it the same as the focal distance, or twice the focal distance?
For small separations of LNBs this is a minor problem, but for bigger distances the effect might be noticeable. And I would like to understand the theory behind it.
Q2.
What should theoretically be the aiming point of the LNBs?
On a straight multifeed bracket you often see them pointing straight towards the dish, on a curved multifeed bracket you often see them pointing towards the middle of the dish.
Thinking about the G-spot of an offset dish: shouldn't the LNBs also in this case split the opening angle in half, and shouldn't the LNBs point to their own horizontal G-spot?
Q3.
What is the most exact way to calculate the distance between LNBs?
I've seen 3 different ways to calculate the distance between LNBs for multifeed installations.
All are dependent on the focal distance (or distance to the G-spot for offset dishes) and on the difference in Azimuth of the two satellites:
a. distance = fG x sin(dA)
b. distance = fG x ( (dA x PI) / 180) (that is: in radials)
c. distance = fG x tan (dA)
[focal distance = fG, Azimuth difference = dA]
In this order they go from smallest to biggest number.
Till about 15 degrees difference in azimuth they have similar outcomes, but with bigger angles the differences become bigger. Which is the best formula for bigger azimuth differences?
Q4.
Extra question: Would the answers to the questions above be different for multifocus dishes, such as Visiosat (Big) BiSat or Maximum E-85?
For purely toroid dishes, I know that the focal line is curved away from the dish, and that the LNBs look away from the middle of the dish. So is a multifocus dish somewhere between a 'normal' dish and a toroid dish? What kind of focal line, where to aim your LNBs?
This has become a rather long post, but I hope to get some good answers, and to understand the principles of multifeed reception better!
Greetz,
A33





 .
.